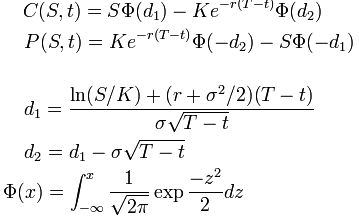Das Black Scholes Modell revolutionierte den Handel mit Optionen, da es das erste genaue Modell war, mit dem man den Wert von Optionen berechnen konnte. Es wurde von Fisher Black und Myron Scholes entwickelt.
Der Grundgedanke dahinter war, dass auf einem effizienten Kapitalmarkt mit jedem risikolosen Investment beliebige Zusammensetzung einer bestimmten Rendite und zwar der risikolose Zinssatz r erzielt wird. Beim Black Scholes Modell besteht dieses risikolose Investment aus einem abgesicherten Portfolio, das aus einem festgelegtem Verhältnis von einer einer long Position und einer short Position von Aktien aufgebaut ist.
Gemäß des CAPM sollte der Ertrag aus diesem risikofreien Investition wie jede andere risikolose Anlage, also r entsprechen. Die folgende Black Scholes Modell gilt unter folgenden Marktbedingungen:
- ein effizienter Markt vorliegt
- Käufe und Verkäufe von Aktien keine Auswirkungen auf Optionen haben
- Informationen sind kostenlos und überall verfügbar
- r ist bekannt und konstant
- Aktienkurse folgen einem random walk
- keine Dividendenzahlungen während der Optionslaufzeit
- Ausübung nur bei Fälligkeit (Europäische Option)
- Transaktionskosten und Steuern vernachlässigbar
- Leerverkäufe erlaubt
- Stückelung möglich
Dabei gilt:
- C= Call, P = Put
- S = aktueller Aktienkurs, r = risikoloser Zinsatz,
- K=Basispreis oder Strike, T-t= Restlaufzeit zum Zeitpunkt t
- Sigma = Volatilität
Vereinfacht ausgedrückt, stellt die Black Scholes Formel daher nichts anderes dar, als die Anwendung des Barwertkonzepts auf unsichere Gewinne. Der Wert der call Option besteht aus der Summe der Barwerte der möglichen Gewinne, gewichtet mit der Eintrittswahrscheinlichkeit. In Letzterem liegt auch das Problem von Black Scholes, denn es wird eine Normalverteilung angenommen, die in der Realität nicht immer zutreffend ist für die Verteilung von Aktiengewinnen. Zum Beispiel vor der Entscheidung ob ein Biotechmedikament für eine kleinere Firma zugelassen wird oder nicht wird der Aktienkurs mit hoher Wahrscheinlichkeit extrem reagieren, je nach Art der Entscheidung, was im Black Scholes Modell nicht erfasst wird. Bei einem solchen Fall ist es auch attraktiver die Option at the money zu halten als die Aktie selber, da das Risiko kleiner ist, aber das upside dasselbe.
Aus der Black Scholes Gleichung kann man auch die „Griechen“ ableiten, die ebenfalls für den Optionshandel wichtig sind, nämlich Delta (Preissensitivität, Art Beta Faktor für Optionen), Gamma, Vega, Theta, Rho und Omega